Associativity vs. Distributivity

July 21, 2014

Associativity vs. Distributivity

Filed under: Racks and quandles — dmoskovich @ 7:04 am

A binary operation $\star$ is associative is $(a\star b)\star c= a\star (b\star c)$ . Examples of associative operations include addition, multiplication, connect-sum, disjoint union, and composition of maps.

A binary operation $\triangleright$ is distributive over another operation $\blacktriangleright$ if $(a\blacktriangleright b)\triangleright c= (a\triangleright c)\blacktriangleright (b\triangleright c)$ . If $\triangleright=\blacktriangleright$ then the operation is said to be self-distributive. Examples of self-distributive operations include conjugation $x^y\stackrel{\textup{\tiny def}}{=} y^{-1}xy$ , conditioning $X|Y$ (assume X and Y are both Gaussian so that such a binary operation makes sense, essentially as covariance intersection), and linear combinations $sx+(1-s)y$ with $s\in \mathbb{R}$ (say), and $x,y$ elements of a real vector space.

Two nice survey papers about self-distributivity are:

J. Przytycki, Distributivity versus associativity in the homology theory of algebraic structures. arXiv:1109.4850.
M. Elhamdadi, Distributivity in Quandles and Quasigroups. arXiv:1209.6518

I won’t survey these paper today- instead I’ll relate some abstract philosphical musings on the topic of associativity vs. distributivity.

Algebraic topology detects information not only about associative structures like groups, but also about self-distributive structures like quandles. I wonder to what extent distributivity can stand in for associativity. Might our associative age give way to a distributive age? Will future science will make essential use of distributive structures like quandles, racks, and their generalizations? At the moment, such structures appear prominently only in low dimensional topology.

Philosophical thesis

I think that there is a philosophical difference between an associative world and a distributive world. The associative world is a geometric world; a world in which space and time are important and fundamental concepts. The distributive world seems different to me. I think that it is a quantum world without space and time, in which only information exists.

Analogous to mass being a manifestation of energy via $e=mc^2$ , so energy may be viewed as a manifestation of information via Shannon/Boltzman entropy. From a physics perspective, there exists the `future physics’ idea that space and time might be emergent, and that the only true fundamental physical quantity is information. Vendral has written a book expounding this point of view. If this idea takes hold, then future fundamental physics will include information physics, and I believe that its underlying mathematics will belong not to the associative world, but rather to the distributive world. I speculate that information physics will some day make essential use of quandles, racks, and related structures.

The associative world is more familiar, so I’ll begin with a survey of the history of the distributive world, followed by a brief survey of both worlds. Then I’d like to compare and contrast them.

Some history

But perhaps there is more in heaven and earth than is dreamt of in associative philosophy. The person credited with this observation is the great American logician C.S. Pierce when in 1880 he concluded:

These are other cases of the distributive principle… These formulae, which have hitherto escaped notice, are not without interest.

For the next century or so, like stray ants who don’t follow paths to establish food sources, there were occasional bursts of realization that distributivity might be fundamental. Notable among the mavericks is M. Takasaki. Alone and isolated as a fresh Japanese math PhD in Harbin during wartime, Takasaki defined an involutive quandle in 1942 as an abstraction of the geometric idea of a symmetric linear transformation. Takasaki envisioned his self-distributive `keis’ as alternatives to groups, but his dream is still largely unrealized. In 1959 another group of mavericks, John Conway and Gavin Wraithe, discovered quandles and racks whose operations were abstractions of the conjugation operation in group theory. But it was only in 1982, with the work of Joyce, and another great independent discoverer Matveev, that quandles and racks entered the mathematical consciousness. Other independent thinkers who discovered or rediscovered such structures (racks, in this case) include Brieskorn and Kauffman. There were ideas about using quandles in the context of geometry (Takasaki), singularity theory (Breiskorn), and symmetric spaces (Joyce), but I think that quandles and suchlike only really ever took hold in low dimensional topology.

From the knot theorist’s perspective, quandles and racks were popularized by Fenn, Rourke, and Sanderson’s 1992 discovery of rack cohomology (the quandle version is due to Carter et.al., and the history is explained in his survey). It turns out that algebraic topology works just fine when associativity is replaced by distributivity, and quandle cocycles yield computable knot invariants. Algebraic topology of quandles and racks has become a bit of a subfield inside low dimensional topology, and this is more or less the only quasi-popular use of quandles of which I am aware.

Note: quandles and racks are only part of the mathematical consciousness of low-dimensional topologists! Physicists, biologists, chemists, computer scientists, engineers, and the rest of humanity don’t really know what a quandle is. I think that we’re a few steps ahead of the pack.

Associativity: A world of space and time

Viewed broadly enough, I think that every associative operation is an abstraction of one or more of the following archetypes:

Addition: The archetypal geometric picture for addition is concatenation of segments of specified lengths. To add natural numbers $a$ and $b$ , start with a number line, represent the number $a$ by the segment $\overrightarrow{0a}$ , mark a second point at distance $b$ from point $a$ in the positive direction representing $b$ as $\overrightarrow{a(a+b)}$ , and concatenate the two line segments to represent $a+b$ by the concatenated directed segment $\overrightarrow{0(a+b)}$ . Associativity is seen in the geometry (the space), in that $(a+b)+c= a+(b+c)$ , and both are represented by the same directed segment $\overrightarrow{0(a+b+c)}$ .
Multiplication: The archetypal geometric picture for multiplication is to fill a cycle by a cell. To multiply natural numbers $a$ and $b$ , represent $a$ by the directed segment $\overrightarrow{(0,0)(a,0)}$ along the x-axis and represent $b$ by the directed segment $\overrightarrow{(0,0)(0,b)}$ along the y-axis, and form the rectangle $(0,0)(a,0)(a,b)(0,b)$ . The product $ab$ is visualized as the area of the rectangle (the 2-cell) in the upper right quadrant whose boundary is the above rectangle. Associativity is seen from the fact that $(ab)c=a(bc)$ both measure the area of the same cube in Euclidean 3-space.

In the associative world, it makes sense to represent objects by 0-cells and maps by 1-cells. Data structures can sensibily be represented using labeled graphs. A composition of maps from an object represented by a vertex $v$ to an object represented by a vertex $w$ on a graph is represented by a path on the graph between $v$ and $w$ . It makes sense to represent a composition of maps in this way thanks to associativity- there is no need for brackets along the path. Maps between maps can be represented by directed higher cells, sort of like our geometric picture for multiplication. Again, this makes sense thanks to associativity.

The claim that I am making is that formalisms such as category theory and graph theory are native to the associative world. So too classical probability theory. Probabilities are added and multiplied, and they are always between $0$ and $1$ . So too, the theory of computable functions relies on associative compositions.

Distributivity: A world of information

Let’s consider the following archetypes for distributive operations:

Convex combination: Our first archetype is $a\triangleright_s b \stackrel{\textup{\tiny def}}{=} sa+(1-s)b$ with $a,b$ elements of a real vector space, and $s\in[0,1)$ .
Conjugation: The second archetype is $a\blacktriangleright b \stackrel{\textup{\tiny def}}{=} b^{-1}ab$ .

Neither of these operations are associative in general. For example,

$(0\triangleright_{0.5} 1)\triangleright_{0.5} 1 = 0.75 \neq 0.5= 0\triangleright_{0.5} (1\triangleright_{0.5} 1)$ .

Both operations have natural archetypes in the world of information (their best-known archetypes are in low dimensional topology of course). One archetype for convex combination is from Bayesian statistics. I estimate the mean of data based on a sample, and I obtain a number $a$ . But I have a prior belief that the mean should actually be $b$ . Based on external information (e.g. the number of elements in the sample and my choice of standard of `absolute credibility’), I compute a constant $s\in [0,1)$ , and my updated estimate becomes $a\triangleright_s b$ . Fusion operations satisfy $(a\triangleright_s b)\triangleright_t c= (a\triangleright_t c)\triangleright_s (b\triangleright_t c)$ .

I can view convex combination as `mixing’; I mix $s$ units of $a$ with $1-s$ units of $b$ .

An archetype for conjugation might quantum interference, where quantum evolution of density operator conjugates it by a unitary operator. So `interaction’ is convex combination, and `evolution’ is conjugation…

It doesn’t make much sense to represent words in Distibutive Non-Associative (DNA) structures using concatenated edges in labeled graphs, because concatenating edges would not correspond to a well-defined composition of operations (because of non-associativity). There are still notions of Cayley graphs for quandles and racks (e.g. Chapter 4 of Winker’s thesis); I don’t feel qualified to comment on these.

The natural way to represent words in DNA structures, I would think, would be to walk along (modified) tangle diagrams. A Reidemeister III move on tangle diagrams coloured by distributive structures makes sense, because $(x\triangleright y)\triangleright z= (x\triangleright z)\triangleright (y\triangleright z)$ :

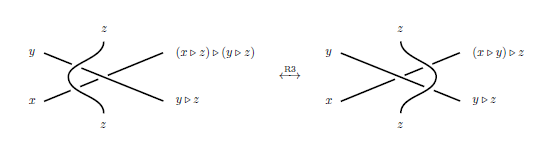
An R3 move.

One idea behind tangle machines is to make use of this fact to do distributive algebra on tangles. So, while for an associative operation one might diagrammatically represent $2+3-4$ in some way like this:

2+3-4.

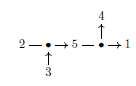
In a distributive world we might represent $\left(0\triangleright_{\frac{2}{3}}3\right)\triangleleft_{\frac{2}{3}} 7$ maybe like this:

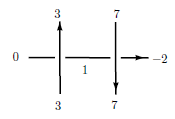
Word in a self-distributive structure.

Is there a DNA (Distributive Non-Associative) analogue to category theory, where morphisms distribute but don’t have associative composition? I wonder… I also wonder whether quantum probability, suitably formulated using convex combination and conjugation operations, would be a valid DNA analogue to probability. If we take Reidemeister 2 seriously, and apply it to the DNA structure of Gaussian distributions whose operation is conditioning, we have to define `unconditioning’ X by Y, and the resulting probability might be negative. Classically this makes no sense, but from a quantum perspective it’s fine, and even natural; it feeds my confirmation bias for the philosophical thesis we are considering. Consider the following quote by Feynmann:

The only difference between a probabilistic classical world and the equations of the quantum world is that somehow or other it appears as if the probabilities would have to go negative.

Associative vs. self-distributive tangle formalisms

Most quantum topology of tangles is actually associative, in that we speak of the category of tangles, whose operation is stacking. Objects are tangles with tops and bottoms:

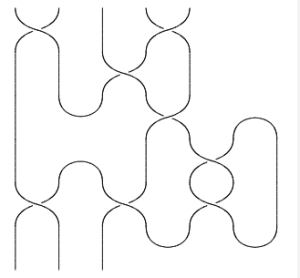
A tangle to stack

Stacking is an associative operation. Via a TQFT formalism, braided monoidal bla bla bla categories give rise to tangle invariants and to knot invariants.

Dror Bar-Natan suggested that this might not really be the right way to think about tangles. Tangles should not have `tops’ and `bottoms’- such information certainly does not exist topologically. Instead, endpoints of tangles should be marked points around a disc (more generally a disjoint union of spheres with holes):

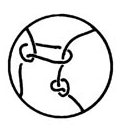
A tangle in a disc

Surprisingly, this disc, which (partially following Bar-Natan) I think we should call the `firmament’, is quite important: See Dror’s “cosmic coincidences” talk.

You then concatenate by connecting two endpoints, and extending the firmament appropriately. This way of thinking is behind Dror’s Khovanov homology work, and current work on various w-knotted objects by him and collaborators.

A major difference between the “stacking” worldview and the “circuit algebra” worldview is that the former views a tangle as a morphism from data stored in the “boundary points at the bottom” to data stored in the `boundary points at the top”. So a tangle encodes an operator (reference: Chapter 3 of Ohtsuki’s book Quantum Invariants). But in the latter worldview, a tangle just encodes some relationship between a bunch of data at endpoints. In this worldview, a tangle cannot encode a mapping in any meaningful sense- this worldview does not support the idea of operator invariants of tangles. This worldview isn’t imposing any non-topological artificial structure on tangles. All it has are the Reidemiester moves, including Reidemeister III. So tangles in this sense are a distributive-world structure.

As an example, let’s consider a single crossing. When tangles express morphisms to be stacked, this `represents’ an R-matrix representing a linear transformation from a vector space $V\otimes V$ to itself. Bottom happens before top, and there’s an implicit time axis. But with no up-down information, it represents a transition from one undercrossing arc to the other by way of an overcrossing arc, $(a,b)\mapsto a\triangleright b$ . No braided monoidal categories anywhere it sight.

Having tops and bottoms to tangles is nice because associative structures tend to be more amenable to explicit computation. Computing in a quandle is usually very hard, perhaps because the Turing machine formalism itself belongs to the associative world. My vague thought is that we can probably do a lot better in the future using different sorts of (probabilistic?) tools… but that’s a speculation for another day. I also think that distributed and parallel computing could provide better ways to compute in distributive structures, and may in turn have distributive algebraic models (Marius Buliga has some work in this direction: e.g. Chemlambda, joint with Louis Kauffman).

Distributive analogues to associative structures?

Although people have began looking at the distributive world only quite recently, it’s already rife with terminology. The more this world is explored, the more terminology there will be, so I’d just like to point out some parallels. Recalling some axioms, consider the following axioms on a set $Q$ with a set of binary operations $B$ :

Idepotence: $a\triangleright a =a$ for all $a\in Q$ and for all $\triangleright\in B$ .
Injectivity: If $x\triangleright b= a\triangleright b$ for some $b\in Q$ and $\triangleright\in B$ , then $a=x$ .
Distributivity: $(a\blacktriangleright b)\triangleright c= (a\triangleright c)\blacktriangleright (b\triangleright c)$ for all $a,b,c\in Q$ and $\triangleright,\blacktriangleright\in B$ .

If $B$ contains only one element $\triangleright$ , and assuming that $\triangleright b$ is also surjective for all $b\in Q$ , we have the following cases.

If $\triangleright$ is both distributive and idempotent then you’re looking at a spindle.
If $\triangleright$ is distributive and injective then you’re looking at a rack.
If all three, then you’re looking at a quandle.
Only distributive and you’ve got yourself a shelf.

Lots of operations and you might add words like multi-, so you have multiracks, multiquandles, multishelfs… or maybe G-families of quandles, or irq’s, or whatever.

Staring at these DNA structures though, they look quite parallel to familiar associative structures. Injectivity parallels invertibility of elements (i.e. it tells us that $\triangleright$ is left-invertible) and distributivity parallels associativity. I’m not sure what the parallel associative concept to idempotence is (idempotence involves both the element $a$ and the operation $\triangleright a$ ), but I think it might be orthogonality; because $a\triangleright a =a$ reminds me of $M\bar{M}^t=I$ in orthogonal groups. Also, conjugation distributes over convex combination, but not the opposite. We might therefore think of convex combination as being parallel to addition, and conjugation as parallel to multiplication. So, using the adjective `DNA’ for `distributive non-associative’, a quandle might be a `DNA orthogonal group’, a rack might be a `DNA group’, if you have both conjugation and convex combination, maybe you have a `DNA near-field‘.

Why would you use a structure like that? Well, as an example of how it might be useful, here’s an AND Gate without trivalent vertices, where $A_0\stackrel{\textup{\tiny def}}{=} \left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right)$ and $A_1\stackrel{\textup{\tiny def}}{=} \left(\begin{matrix}1 & \phantom{-}0 \\ 0 & -1\end{matrix}\right)$ stand in for the digits $0$ and $1$ correspondingly. The operations $\triangleright_s$ are convex combinations, and $\blacktriangleright$ is conjugation.

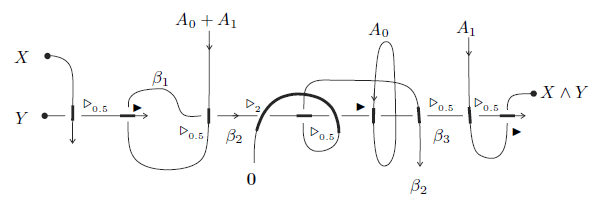
A tangle simulating an AND gate.

It seems to be very natural to consider structures where $B$ has lots of elements- it doesn’t inhibit their algebraic topology, it occurs naturally in our archetypes (in the Bayesian probability archetype, to expect all `new’ information to have the same credibility is unnatural; see also Buliga’s work on irq’s, emergent algebras, and related structures- all DNA structures HERE and HERE), and it allows us to construct various topological invariants such as invariants of knotted handlebodies (“A G-family of quandles and handlebody-knots” by A.Ishii, M. Iwakiri, Y. Jang, and K. Oshiro).

The term `DNA’ suggests that distributive non-associative structure are in some way fundamental (like DNA is fundamental to cells in living organisms), and I think that they are. There are some simple transforms between the associative world and the distributive world too: Given a group, you can look at it’s associated conjugation quandle. Conversely, automorphisms of a quandle form a group. In another direction, you can represent a tangle diagram by a graph for example by representing each arc as a vertex, drawing edges from the vertex representing the overcrossing to the two vertices representing undercrossings, and drawing an edge between the undercrossings. By doing this you’ve thrown away all your symmetries- graphs are rigid and there are no Reidemeister moves on graphs. This construction is also partially reversible.

Conclusion

I think there’s a whole distributive world waiting to be discovered, and we’re just looking at the tip of the iceberg. I can’t wait to see these distributive structures play a role outside low dimensional topology, in other parts of mathematics and in other sciences!

Leave a Comment »

No comments yet.

RSS feed for comments on this post. TrackBack URI

	Jorge Antonio Gonzál… on A celebration of diagrammatic…
	Large scale properti… on 3-manifold groups are known,…
	ianagol on Virtual Low-dimensional Toplog…
	Ken Perko on Virtual Low-dimensional Toplog…
	Robert Osborne on The face manifold
	QC Coronavirus Editi… on Finding clusters in data
	Paulo Ney de Souza on Labeling figures in LaTeX
	Nathan Dunfield on Labeling figures in LaTeX
	Paulo Ney de Souza on Labeling figures in LaTeX
	Isotopy in dimension… on Isotopy in dimension 4

Low Dimensional Topology

July 21, 2014