The Alexander Polynomial as a Quantum Invariant: Part 3

March 4, 2010

The Alexander Polynomial as a Quantum Invariant: Part 3

Filed under: Knot theory,Quantum topology — dmoskovich @ 3:18 am

My original intention for this post was to summarize Chapter 2.3 and Appendix C of Quantum Invariants by Tomotada Ohtsuki, with some commentary. But it looks like an opaque calculation to me at the moment- calculate the R-matrix of the Alexander polynomial from its Skein relation, and lo-and-behold it coincides with the R-matrix you get from a certain representation of the braid group on $n$ strands to $V^{\otimes n}$ , where $V$ is a 2-dimensional vector space over $\mathbb{C}$ . It’s mathematics I can calculate as opposed to mathematics I understand (to some extent anyway), and I’d much rather blog about the latter than about the former. Ohtsuki writes it up better than I ever could anyway.
Luckily, thanks to a number of very good reader responses, I can post instead about two very beautiful and profound ideas, which, while falling short of conceptually explaining the quantum nature of the Alexander polynomial (to my eyes anyway), certainly point very much in the right direction.

Let’s begin with the reference Ryan sent me:

A Lagrangian Representation of Tangles by D. Cimasoni and V. Turaev.

This paper extends the Burau and Gassner representations from braids and string links to tangles. It gives rise to the Alexander polynomial of the closure if the tangle is straight, meaning that it has no closed components. In this way, it explains the local nature of the Alexander polynomial (restricted to straight tangles at least) in a conceptual way. But, because the tangles must be straight, and you have to take the closure “by hand”, it doesn’t really answer the question. The “spinning” operation of taking the closure isn’t built into the construction. In any event, this is rather a large step in the right direction, I think, and any conceptual explanation worth its salt of the quantum nature of the Alexander polynomial should surely recover Cimasoni-Turaev.
The tools used are completely classical, although the setup is one which quantum topologists use all the time. Consider your tangle $T$ to live inside a cylinder $D^2\times [0,1]$ , and let $X$ denote $D^2\times [0,1]- nbd(T)$ (the complement of the tangle in the cylinder). Perturb a height function so that at each height slice you have a crossing, a cup, or a cap. Think of this as a cobordism between two oriented discs with holes $D_\epsilon := D^2\times{1}$ and $D_{\epsilon^\prime} := D^2\times{0}$ . In physics, the cobordism $X$ might be a time evolution from one state of the world to another, your cup might be the birth of a particle-antiparticle pair, and the cap might be their annihilation. As far as the Alexander polynomial and suchlike invariants are concerned, we only care about homology (by the way, in my opinion this implies that a good explanation of anything to do with the Alexander polynomial of a knot should work for a homology $S^1$ embedded in a homology $S^3$ ).
In think I’d like to think about what Cimasoni and Turaev do next in terms of homology wiith local coefficients (thanks one more time, Ryan!). Let $\pi:\tilde{X} \longrightarrow X$ be the infinite cyclic covering space of the knot complement, and consider $H_1(X; s)$ where $s$ is the bundle of groups where the fibre over a point $x \in X$ is $H_0(\pi^{-1}(x))$ . Starting with the case that $T$ is a braid, as a warmup to the key idea, $T$ induces a homomorphism $f$ from $H_1(D_\epsilon; s)$ to $H_1(D_{\epsilon^\prime};s)$ , acting on homology classes sort of like an egg-beater. This homomorphism turns out to be a unitary isomorphism, and mapping $T$ to the matrix representing $f$ gives rise to the Burau representation of the braid group. Next consider $T$ to be a string link (strands go from bottom to top, but not necessarily monotonically). This time you have to localize local coefficients, but after you do that, the same construction again gives a unitary homomorphism $H_1(D_\epsilon; \hat{s})$ to $H_1(D_{\epsilon^\prime}; \hat{s})$ , and mapping $T$ to the matrix representing $f$ gives Le Dimet’s extension of the Gassner respresentation.
In both these cases, a cobordism $(X,D_\epsilon,D_{\epsilon^\prime})$ induced a homomorphism from the homology of the bottom disc to the homology of the top disc, with appropriate local coefficients. But in general a cobordism won’t do that. But a standard result about concordance is that what a cobordism will do is that the kernel $N(T)$ of the inclusion homomorphism $H_\ast(D_\epsilon)\oplus H_\ast(D_{\epsilon^\prime})\longrightarrow H_\ast(W)$ will induce a morphism between $H_\ast(D_\epsilon)$ and $H_\ast(D_{\epsilon^\prime})$ (coefficients in the bundle of groups $s$ ). This kernel is Lagrangian with respect to the intersection form on homology (their definition of Lagrangian is a bit algebraic, but it means just what you think it means- maximal isotropic).
This idea reminds me of chess players like Karpov and Capablanca- the moves look simple and obvious, but only after they have been played. That the idea looks so obvious in retrospect seems to me to be a sign that it is the right one, and a testimony to the genius of its authors.
Then, of course, you have the details- $N(T)$ needs to be free, or the algebra doesn’t seem to work. Therefore $T$ needs to be a straight, and the “spinning operation” needs to be worked in by hand. So it fails to be an explanation of why the Alexander polynomial of a knot or of a link is a quantum invariant, or at least has the right locality properties (it doesn’t bother calculating the R-matrix, although it’s obvious how to do so).

The second reference I was sent, by one of it’s authors (thanks!) is

The Alexander polynomial via topological quantum field theory. by C. Frohman and A. Nicas, in Differential geometry, global analysis, and topology (Halifax, NS, 1990), 27–40, CMS Conf. Proc., 12, Amer. Math. Soc., Providence, RI, 1991.

It’s a bit terrifying to try to summarize the main ideas here when the author might well be reading what I write… well, blogging is really all about advertising one’s ignorance to the world anyway, so here goes…
Consider a knot $K\subset S^3$ . Frohman and Nicas consider the Alexander polynomial to as an invariant of the homology of a Seifert surface (independent of the choice of Seifert surface), so they choose a Seifert surface $F$ with bicollar $F\times I$ whose complement is $H:= \overline{S^3-(F\times I)}$ . Consider $H$ as a cobordism between $F_0:=F\times \{0\}$ and $F_1:=F\times \{1\}$ . You now have the inclusion $H_1(F_0)\longrightarrow H_1(F_0\cup F_1)\longrightarrow H_1(H)$ which is represented by the Seifert matrix (after you choose bases for homology). This is pretty much the classical setup for the Alexander polynomial.
What Frohman and Nicas do now, which is very interesting, is to reproduce this setup on the Jacobian of the Seifert surfaces, that is the $U(1)$ -representation variety $J(S)=\mathrm{Rep}(\pi_1(S),U(1))$ . If $S$ is not connected, $J(S)$ is the cartesian product of these over its connected components. It turns out that $H_1(S)$ and $H^1(J(S))$ are isomorphic, as are $H_1(H)$ and $H^1(J(H))$ . This is either miraculous or obvious, depending how you think about it- obvious because $U(1)$ is just the circle group, and this is kind-of the universal coefficient theorem, and miraculous because it lets you construct the Alexander polynomial by using, instead of homology of Seifert surfaces, cohomology of their Jacobians. A graded Lefshetz trace takes the place of taking the determinant, their equivalence proved by linear algebra. It bothers me that the linear algebra has to take place over $\mathbb{R}$ (or at least $\bar{\mathbb{Q}}$ ) for this linear algebra to work, because we need to take square roots, although Kerler makes it work over $\mathbb{Z}$ , using a bit of representation theory (I think).
By the way, I first read Kerler’s paper in 2002 for a reading course on Reidemeister torsion at Tokyo University. While reading it, I got tired of the use of acronyms like TQFT in mathematics and physics, and resolved to call TQFTs topoquafts. Therefore, because a blog is a good place to showcase one’s silliness, I think I shall continue to call them topoquafts in this post.
So why is representing the Alexander polynomial in terms of Jacobian varieties a good thing? Because you can obtain a topoquaft from this construction in the following way. First, perform $0$ -surgery on the knot in $S^3$ , making the two copies of the Seifert surface into a pair of closed surfaces $\partial_{\text{in}}M$ and $\partial_{\text{out}}M$ in a $3$ –manifold $M$ . So now $M$ is a cobordism between closed surfaces. The construction is easier to describe (see Kerler) when $H_1(\partial M; \mathbb{Q})\longrightarrow H_1(M,\mathbb{Q})$ is an epimorphism, so let’s restrict to that case. Then $j:J(M)\longrightarrow J(\partial_{\text{in}}M)\times \partial_{\text{out}}M$ is a half-dimension immersion (is it Lagrangian with respect to some natural non-degenerate skew-Hermitian form?). So the top form $\pm[J(M)]$ defines a middle-dimensional homology class in $H_\ast(J(\partial_{\text{in}}M);\mathbb{R})\otimes H_\ast(\partial_{\text{out}}M;\mathbb{R})$ . Using Poincare duality, this space is isomorphic to the space of linear maps between homology rings of the Jacobian varieties. The functor which associates to $M$ the linear map which comes from $j_\ast (\pm J(M))$ now satisfies the axioms of a topoquaft. In general, if $H_1(\partial M; \mathbb{Q})\longrightarrow H_1(M,\mathbb{Q})$ fails to be onto, Frohman and Nicas consider the (graded) intersection number of the Jacobian of a thinkened Heegaard surface $\Sigma$ for $M$ with the Jacobian for handles separated by that surface. This makes the Alexander polynomial look very much like the Casson invariant, which is good!
This construction puts the Alexander polynomial firmly inside the world of quantum topology, but doesn’t explain why it is a quantum invariant in the sense discussed in the last post- namely, it can’t be calculated from decomposing your knot into crossings, cups, and caps in any obvious conceptual way, and it doesn’t even give rise to an $R$ -matrix. I don’t even see how it extends to tangles, string links, and braids. Actually, Kerler shows that you can recover an $R$ -matrix from the Frohman-Nicas topoquaft by proving its isomorphism with the Hennings topoquaft, which does give all these good things, for the non-semisimple Hopf algebra $\mathbb{Z}/2\ltimes \bigwedge ^\ast \mathbb{R}^2$ . This is a horrible Hopf algebra to have to work with. Worse still, Kerler’s proof is a calculation and imparts no conceptual understanding (to me anyway) as to why it should hold. In this sense, Frohman-Nicas both completely answers our question about how to see the Alexander polynomial as a quantum invariant, and completely fails to answer it. But it’s a beautiful and profound idea in any case.
What strikes me most about this paper is that nobody besides Kerler seems to have followed up on it, despite the fact that it’s almost 20 years old and that the ideas in it are so natural. There are so many really silly, naive questions which I have, such as:

Does this work in any setting where one constructs the Alexander polynomial using a Seifert surface? How about homology boundary $n$ -links in a homology $(n+2)$ -sphere?
Can you get rid of the Seifert surface? I have some silly ideas which don’t seen to work about this…
Categorify. Surely. This setting is pure Knot Floer Homology Land.
As the authors mention- different gauge groups! Maybe stuff like $sl(1\mid 1)$ .

So, in conclusion, I’m surprised to say that Ryan’s request for a conceptual explanation of why the Alexander polynomial is a quantum invariant (in the sense I mean, at least) seems to be an open problem. And a very interesting one at that, if you ask me!

Comments (5)

5 Comments »

Nice blog.
The first question, does it work in any dimension? There is something peculiar about oriented three-manifolds,
in the long exact sequence $(M, \partial M)$ , at $H_2(M,\partial M)\rightarrow H_1(\partial M)\rightarrow H_1(M)$ in that Poincare duality means that the two maps in the sequence are adjoints to one another. This is what causes the image under restriction of the representations of the three manifold group to tend to be a Lagrangian subspace of the Symplectic manifold that is the characters of the surface $\partial M$ , that does not carry over to higher dimensions, so for n>3 you don’t get half dimensional subspaces.

More generally in dimension three, Jana Archibald has a tangle multivariable Alexander invariant that is an element of an exterior algebra. It is most likely related to the construction in the paper with Andy, though her approach is via Fox Calculus. A really nice feature of her work is that she is able to annihilate the ambiguity in sign by tensoring with a simpler computation that suffers from the same ambiguity.

The other direction this goes is probably more familiar to you, geometric quantization. The paper I saw along these lines using the Jacobians was by Louis Funar, back in mid 1990s. More recently Razvan Gelca and Alejandro Uribe have looked at this set up from the viewpoint of geometric quantization and gotten some really nice formulas.

Also, as long as we are talking about the Alexander polynomial as a quantum invariant, we could talk about the twisted Alexander polynomial. Recently, Oliver Dasbach, Heather Russel, and Moshe Cohen have developed a dimer model for computing the twisted Alexander polynomial using representations into finite groups. This means there is a skein relation, and no doubt an R-matrix. It would be interesting to understand the R-matrices conceptually, starting with the finite group.

The twisted Alexander polynomial as a quantum invariant is really provocative, as L\”{u}ck’s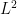 $L^2$ -torsion of a three-manifold, which along with Lott, he proved to be hyperbolic volume is computed via Fox Jacobians, so it is a close relative. If you could see that as coming from an 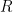$R$ -matrix, or as the semiclassical limit of 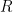$R$ -matrices, you might have a shot at proving the volume conjecture.

Another road that no one has taken is that character varieties of surface groups, tend to be complex projective varieties, so that their Dolbeaut cohomology groups have a very rich structure.
Is there some way of using the $(p,q)$ filtration from this theory to define more sensitive invariants of knots that detect deeper data than the Alexander polynomial?

Thanks for the gracious response to my remarks.

Comment by Charlie Frohman — March 4, 2010 @ 7:45 am | Reply
- You put your finger precisely on my primary current research interest. Seeing twisted Alexander polynomials as quantum invariants (as 1-loop parts of a twisted rational Kontsevich invariant) is something I’ve been looking at for a while. I don’t have anything concrete about twisted Alexander polynomials that I’m ready to post about in a blog yet, but that was an extremely perceptive comment!
  
  Comment by dmoskovich — March 6, 2010 @ 9:47 am | Reply
- Another question which I have is how such a construction would work for links. One would be forced to do it without reference to a Seifert surface.
  
  Comment by dmoskovich — March 8, 2010 @ 9:03 am | Reply
Two typos, I have the wrong dimension on the homology group of the boundary of the three manifold , it should be first dimension. Next, I said representation varieties of surface groups tend to be projective varieties, when I meant character varieties of surface groups.

Comment by Charlie Frohman — March 4, 2010 @ 7:57 am | Reply
- I editted your comment to incorporate these corrections.
  
  Comment by dmoskovich — March 6, 2010 @ 6:03 pm | Reply

RSS feed for comments on this post. TrackBack URI

	Jorge Antonio Gonzál… on A celebration of diagrammatic…
	Large scale properti… on 3-manifold groups are known,…
	ianagol on Virtual Low-dimensional Toplog…
	Ken Perko on Virtual Low-dimensional Toplog…
	Robert Osborne on The face manifold
	QC Coronavirus Editi… on Finding clusters in data
	Paulo Ney de Souza on Labeling figures in LaTeX
	Nathan Dunfield on Labeling figures in LaTeX
	Paulo Ney de Souza on Labeling figures in LaTeX
	Isotopy in dimension… on Isotopy in dimension 4

Low Dimensional Topology

March 4, 2010